[円周率]モンテカルロ法で円周率の近似値を

ちょっとしたネタです。
円周率(3.14~~~のやつ)を求めるには膨大な計算が必要というイメージがありますよね。

実は円周率の近似値を出す方法としてモンテカルロ法という手法が知られており、実装も簡単なのでプログラミング学習者向けの演習課題として用いられてたりもします。

ただし所詮は近似値ですので、大体3.14くらいっていうのが分かる程度の精度です。

今回はProcessingを使ってモンテカルロ法で円周率を求める過程を可視化しましたので、そのサンプルコードとアルゴリズムの説明になります。

~~結構大雑把にコードを書いているので綺麗じゃないですが・・・(汗)~~

見出し

1 考え方1 面積比
2 考え方2 命中率こそ面積比率
3 つまり円周率を求めるには・・・
4 Processingソースコード
5 実行経過
6 ということで・・・

考え方1 面積比

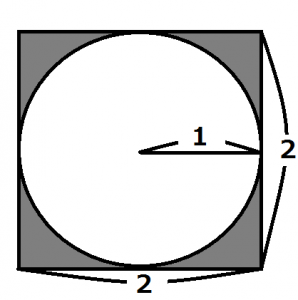
1辺の長さが2の正方形を考えます。
この正方形の面積は
縦 × 横 = 4
です。

続いてその正方形に接する円を考えます。
1辺の長さが2の正方形に接する円の半径は1ですね。
円の面積は
半径 × 半径 × π ですので、
この円の面積は
1 × 1 × π = π
です。

続いてこの正方形と円の面積比率を考えて見ます。
正方形の面積 : 円の面積 = 4 : π
4 × 円の面積 = 正方形の面積 × π
π = 4 × 円の面積 ÷ 正方形の面積
となりますね。

とは言っても円の面積が分かってればそもそも悩む必要は無いわけです。
だから正方形と円の面積比の代わりになるものが必要になるわけですね。

考え方2 命中率こそ面積比率

さて、少し違う図形で考えて見ます。

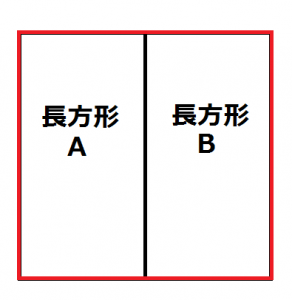
赤い枠の正方形の中に、面積の大きさが等しい長方形Aと長方形Bがあります。
面積の大きさが等しいのですから、この長方形Aと長方形Bの面積の比率は1 : 1ですね。

さて、以下の条件を考えてみてください。

これからあなたはこの赤い枠の正方形に向かって1発の銃弾を放ちます。
あなたの撃つ弾は必ず赤い枠の中に納まります。
しかし、銃弾の軌道は物理法則に従わず、完全にランダムな動きでブレてしまいます。
あなたの撃った銃弾が、長方形Aに当たる確率はいくつでしょうか。

完全にランダムな軌道の弾という定義であれば、長方形Aに当たる確率は50%になりませんか？

長方形Aの面積 : 長方形Bの面積 = 長方形Aへの命中率 : 長方形Bへの命中率
そう・・・
面積比というのはつまり的当ての命中率と考えられるってことですね！！(あくまで例えです)

つまり円周率を求めるには・・・

つまり、下のような図形を用意して・・・

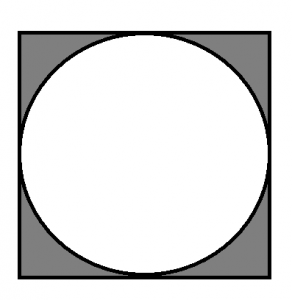
この正方形に向かって銃弾を乱射して、円の中に入った確率を利用すれば円周率が求まりそうです。

先ほど面積比から割り出した
π = 4 × 円の面積 ÷ 正方形の面積
という式を命中率で考え直して
π = 4 × 銃の命中率
と置き換えてみましょう！

もし10発の銃弾を撃って7発が円の中に入ったならば、
命中率は70%なので円周率の近似値は4 × 0.7 = 2.8になります。

もし100発の銃弾を撃って75発が円の中に入ったならば、
命中率は75%なので円周率の近似値は4 × 0.75 = 3.0になります。

もし1000発の銃弾を撃って785発が円の中に入ったならば、
命中率は78.5%なので 4 × 0.785 = 3.14になります。

こんな感じで、一心不乱に銃弾を撃ちまくって円周率の近似値を求めることができますね！

Processingソースコード

Processing2.xでも3.xでも動作すると思います。
このままだとAndroid用に画面サイズをあわせる設定になっているので、もしPC上で実行したい場合は該当箇所をコメント化、コメント解除しないといけません。

今回はビジュアル的にアルゴリズムが分かるように図形を描画しています。
単純に可視化する必要が無い場合には、Processingではなく別の言語で書いたほうが複雑にならなくて良いですね！

※わざわざAndroid用にしているのは、学校のティーチングアシスタントの人や先生が自身のスマホに入れて生徒に教えたりできるかなと思ったためです。

//Androidの解像度対応用
float screenScale;
int baseWidth = 500;
int baseHeight = 800;

// 点の数初期化
int all_points = 0;
int elli_points = 0;
float proba = 0;

// セットアップ
void setup(){
//size(500, 800); //PCから実行する場合はこのコメントを外す

  size(displayWidth, displayHeight, P2D); // PCから実行する場合はこの行をコメントに
  screenScale = min(width/(float)baseWidth, height/(float)baseHeight);// PCから実行する場合はこの行をコメントに

  scale(screenScale);// PCから実行する場合はこの行をコメントに

  // 背景色
  background(255);

  // 灰色の正方形を出力
  fill(220);
  rect(25, 25, 450, 450);

  // 白い円を出力
  fill(255);
  ellipse(250,250,450,450);

}

// 繰り返し処理
void draw(){
  // 速度調整
  frameRate(500);

  // スマホの画面にあわせてスケーリング
  scale(screenScale);// PCから実行する場合はこの行をコメントに

  // 全体の点のカウント
  all_points++;
  
  // ランダムに点を打つ関数の呼び出し
  randpoint();

  // テキストの消去
  noStroke();
  fill(255);
  rect(25, 500, 520, 600); 
  fill(0);
    
  // テキストの描画
  text("すべての点：" + all_points, 25, 520);
  text("円の中の点：" + elli_points, 25, 540);
  text("円周率：" + proba, 25, 560);

}

// ランダムに点を打つ
void randpoint(){

  // 四角形の中に点を打つように座標を調整
  // int型にするのは描画が見やすくするためだが精度は大幅に落ちる
  // rnadomの範囲が25~475なのは描画を見やすくするため
  // 本来は望ましくないので注意
  int x = int(random(25, 475));
  int y = int(random(25, 475));
  stroke(0);
  point(x, y);

  // x軸の半径
  if(x >= 25 && x <= 250){
    x = 250 - x;
  }else{
    x = x - 250;
  }
  
  // y軸の半径
  if(y >= 25 && y <= 250){
    y = 250 - y;
  }else{
    y = y - 250;
  }

  // 半径の2乗より小さければ円の中
   if( (x * x) + (y * y) <= 50625){
   elli_points++;

   proba = 4 * (float(elli_points) / float(all_points));

  }
}

実行経過

①実行開始から間もない頃の状態です。
まだ円周率は3.50と精度は悪いです。

②5000発弱の銃弾を撃った頃。
ようやく円周率として一般的に知られている3.14になりましたね！

③80000発の銃弾を撃った頃。
ついに3.141まできました。理論上はこのアルゴリズムでは無限に銃弾を撃ち続けることで、限りなく正確な円周率に近づくことができますが、コンピュータの乱数は完全なランダムではないですし、そもそも無限に続けること自体が不可能ですので適当なところで切り上げたほうがよいでしょう。
今回は乱数の範囲も狭いので尚更精度は落ちます。